Trees

• Dimension - maximum amount of children a tree node can have (e.g. binary tree - max 2 children)
• Height of a node - amount of levels from the lowest leaf to that node.
• Level of a node - tree layers up to that node from the root. The root is at level 1.

Binary Tree

A very popular kind of tree is a binary tree, where the dimension parameter equals 2.

Binary Search Tree

A binary tree where children with a lesser value are placed on the left, and the children with greater or equal values are placed on the right.

This tree is well known for the Binary Search algorithm that can be applied to it (and to sorted arrays).

Characteristics:

• the smallest value will be the leaf node on the far left
• the greatest value will be the leaf node on the far right
• the tree is Balanced when:
  • the right and left side of the root has rougly the same amount of nodes
  • the height of all leaves is rougly the same
• the Unbalanced tree, in the worst case scenario is like a linked list

Complexity

• Insertion: O(log n) (average); O(n) (worst case, when the tree is highly unbalanced)
• Traversal: O(n)
• Lookup: O(log n) (average); O(n) (worst case, when the tree is highly unbalanced)
• Removal: O(log n) (average); O(n) (worst case, when the tree is highly unbalanced)

AVL

AVL trees are binary search trees that are self-balancing, keeping the Balance Factor at maximum 1 at all times.

Traversal

Pre-order

The parent first, then the children.

Use-cases:

• creating a copy of a tree (with exactly the same placement of nodes)

In-order

The left child is first, then the node, then the right child.

Use-cases:

• sorting elements in the increasing order (must be search tree)

Post-order

The left and right children are first, then the parent node.

Use-cases:

• deleting all nodes of the tree (since we always deal with children first, then the parent)

B-Tree

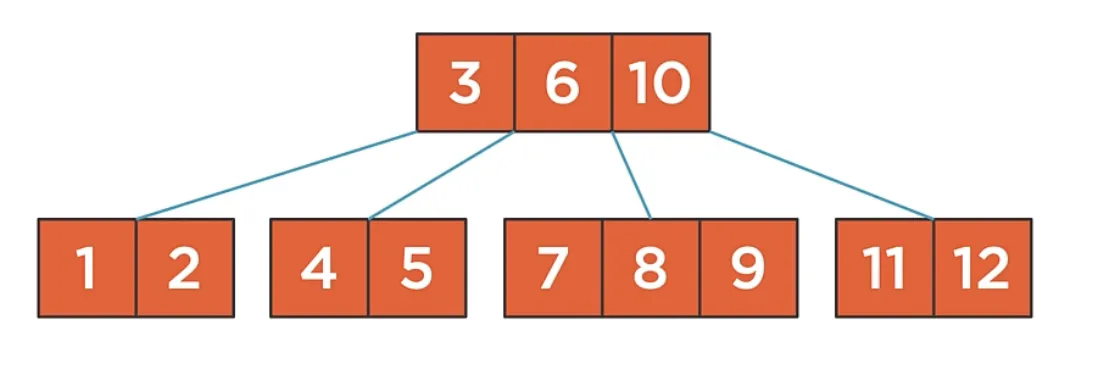
Characteristics:

• A node can have multiple values
• A node can have multiple children
• The children are between the values of the node
• the tree has to be sorted
• For n values in a node, that node can have n+1 children
• Minimal Degree (T)
  • every non-root node has to have at least T children and max 2T children
  • every non-root node has to have at least T-1 values and max 2T-1 values
  • A node with T children and T-1 values is called a Minimal Node
  • a node with 2T children and 2T-1 values is a Full Node
• All leaf nodes should have the same height
• Values can only be added to the leaf nodes

An example of a tree that is not B-Tree:

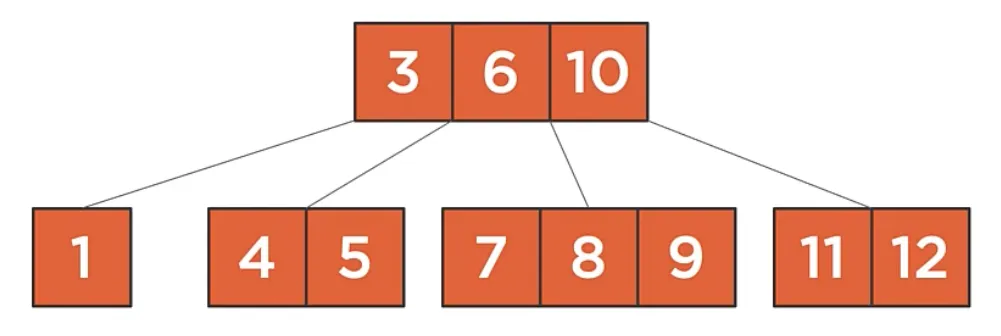
The node “1” does not have enough values (should have at least 2).

Heap

A tree structure where either:

• all children are smaller than or equal to the parent (Max-heap)
• all chidren are greater than or equal to the parent (Min-heap)

Thanks to the above (Heap Property) finding min or max value (depending on a type of heap) is a O(1) operation.

Additionlly:

• The tree must be complete - before starting a new level, the current level needs to be full
• Heap can be stored in an array. We just continuously add the nodes from each level