Fundamentals of Functional Programming

One of the most significant issues in programming nowadays is how to deal with the increasing complexity of the software. Functional Programming is a way to simplify programs.

In FP (opposed to OOP), separating functions from data is natural. Functions encode logic, and data represent inputs and outputs of functions.

In FP, instead of defining steps how to compute something, we define what the result is (imperative vs declarative way).

Other Approaches

First, we had programs written in machine code, or later assembly. They were very explicit and quite difficult to debug, understand, reuse.

Then, Procedural Programming came in giving us a way to abstract some operations into named pieces of code.

Next, the Object-Oriented Programming extended the idea further putting code into objects that hid a lot of implementation details within them. We could treat these objects like black boxes, not caring too much about what they’re doing inside.

It turns out that what objects are doing inside is quite crucial sometimes, especially when parallel programming is introduced. Objects may have some internal state, or they may share some data with other objects. The lack of knowledge about such things leads to bugs in concurrent scenarios. Invoking some method might cause state mutation and we might not even know about it. When running code parallelly we always need to make sure that the classes we use are thread-safe.

The next step that is supposed to make everything sound again, is Functional Programming.

Lambda

The functional approach has its origin in the works of Alonzo Church and his lambda calculus. Church defined a syntax to write (pure) functions. In his approach, a function takes some inputs that are applied into some expression. Any computable problem can be presented using lambda calculus. With that, Lambda calculus is Turing complete, it is actually a different way of expressing the Turing Machine itself, both approaches are equivalent.

A great intoduction to lambda calculus may be found here.

Higher-Order Functions

These are functions that either:

  • accept other functions as inputs
  • return functions as outputs
  • both of the above

Purity

In mathematics, functions don’t have side effects. Based on some inputs, some output is returned. In programming, that’s not always the case. Programs change state.

Functions might be pure or impure. Pure functions are similar to the mathematical functions. They do not rely on or modify any state. Their outputs depend solely on the inputs.

Impure functions can modify (or just read) an external state, and their outputs can depend on some external state as well. They are much harder to reason about, test and they might now work as expected in concurrent scenarios.

Pure functions ALWAYS return the same output for the same input. Functional programs may be optimized with:

  • parallelization - different threads can run functions, and no conflicts will appear.
  • lazy evaluation - only evaluates outputs when needed
  • memoization - caching of results for performance gains

These techniques are not straightforward with impure functions.

Functors

When a value is wrapped in some container (like an Option or IEnumerable) we can’t apply functions to it:

Increment(Some(3)) //doesn't work

This is where Map comes in. It allows us to extract the value from a container and apply a function to it. It returns a functor a well.

Some(3).Map(Increment); //Some(4)

A type for which a Map function (Select in C#) is defined is called a functor. Functors include:

  • collections (or in general IEnumerable)
  • Option

Functors have some inner values to which a function can be applied. A map can be represented as follows:

(C<T>, (T -> R)) -> C<R>

C<T> is a functor.

Map vs ForEach

Map is to be used with functions that have no side-effects, while ForEach is to be used with side-effect function. Example:

var names = new string[] { "Andy", "John", "Jules" };
names
  .Map(n => $"Hello {n}") // pure function
  .ForEach(WriteLine);    // impure function

Map takes a Func, while ForEach takes an Action. ForEach does not return anything.

Map vs Do

We should also consider a Do function (sometimes called Tee or Tap). It is supposed to be used whenever we need to do some side-effect in the middle of a data flow. We could use Map for that as well, but Map shouldn’t be used when side effects are involved.

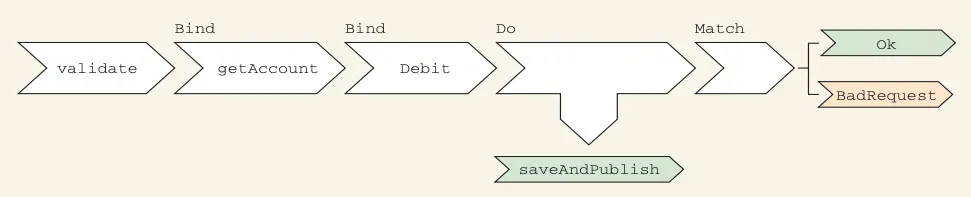
Do invokes some provided action and returns the provided value; the flow may be continued.

Monads

Bind

A Bind function (SelectMany in C#) is useful to flatten lists of lists.

Bind can be represented as follows:

(C<T>, (T -> C<R>)) -> C<R>

A type that has a Bind method is a monad.

Example:

record Pet(string Name);
record Person(string Name, IEnumerable<Pet> Pets);


var people = new[] {
  new Person("George", new List<Pet>{ new Pet("dog"), new Pet("cat") }),
  new Person("Peter", new List<Pet>{ new Pet("hamster") }),
  new Person("Jady", new List<Pet>{ }),
}


var animals = people.Bind(p => p.Pets); // ["dog", "cat", "hamster"]

A Map would return a list of lists. Bind is much more suitable here. The Person[] type is a monad.

Return

A monad must also have a Return function defined. It’s a function that wraps a “normal” value T into a monadic value C<T>.

Return can be represented as follows:

T -> C<T>

An example of a Return function could be a function that turns items into a list, or a Some method of Option.

Regular and Elevated Values

In general, in our programs, we’re dealing with either regular values or elevated values.

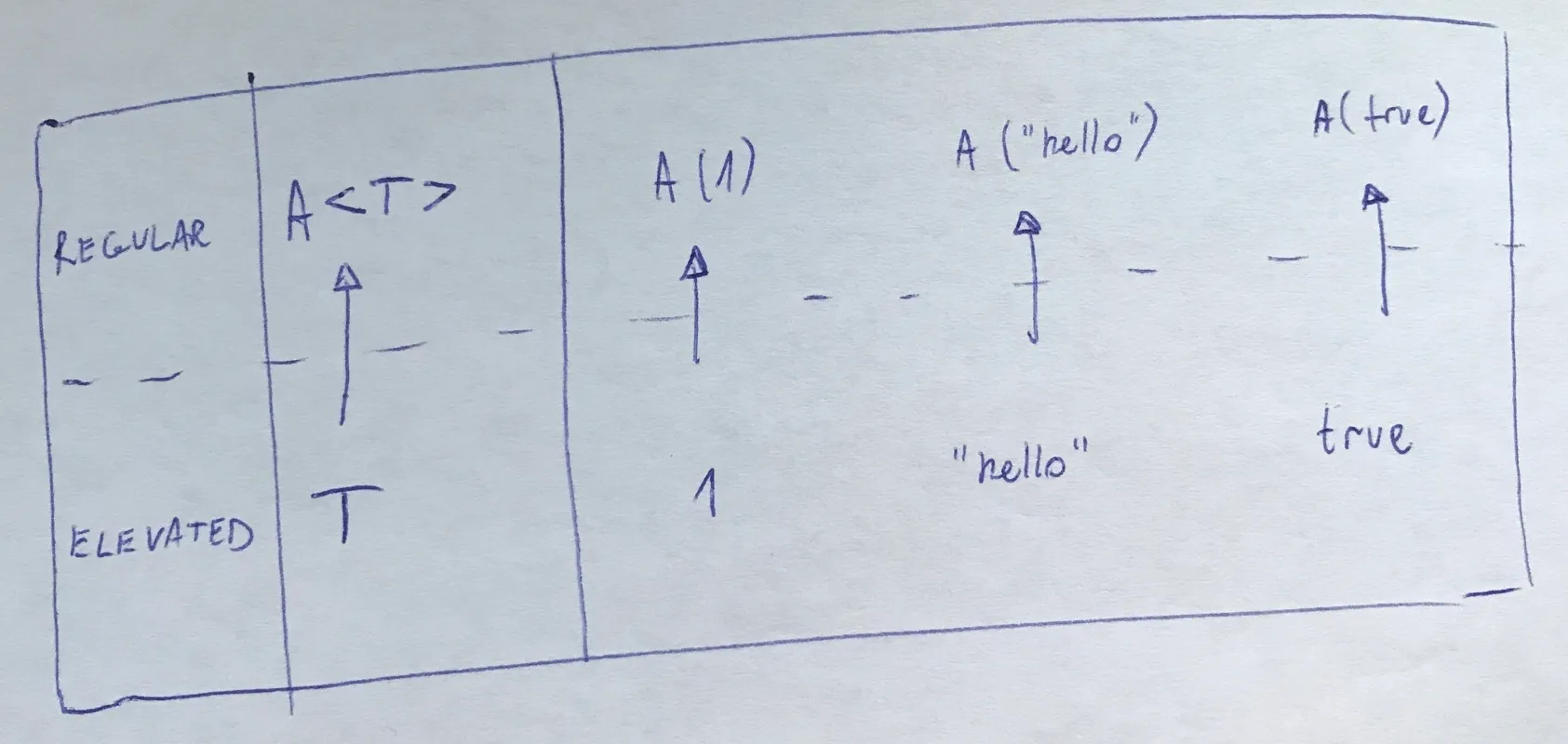
NOTE: The image above has regular/elevated naming reversed. Sorry, my bad!

“Primitive” data types like int, string, bool are regular values. The types that contain other types are elevated values (List<T>, Task<T>, Option<T>). Note that the regular values do not actually need to be primitive data types, they can also be instances of classes like Person or whatever. It’s just a simplified view of the matter.

We can look at various functions that operate on data as either:

  • returning the same level of abstraction
  • crossing abstraction

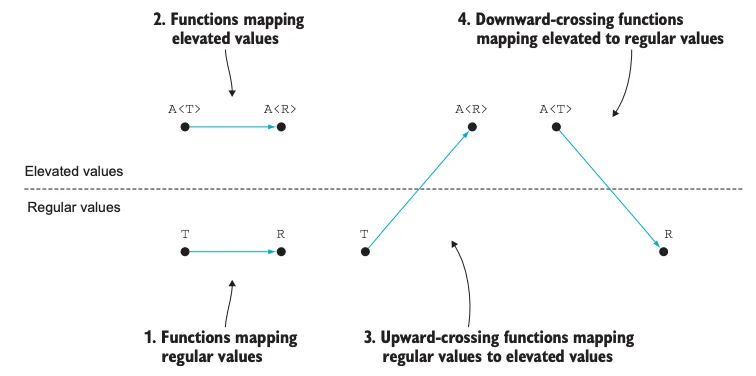
Examples:

  1. (int i) => i.ToString()
  2. (users) => users.Filter(u => u.LoggedIn)
  3. Task.CompletedTask(task)
  4. numbers.Sum()

Map and Bind

Using this classification, we can look see the following relations:

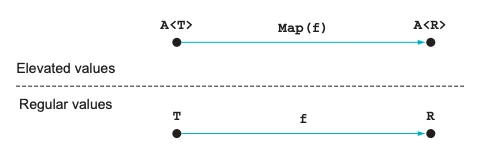
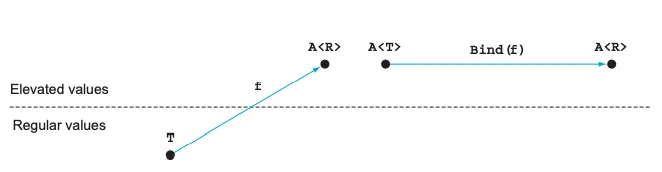
The functions accepted by these two functions differ in the fact that Bind requires a function that crosses the abstraction upwards.

Reducing a list to a single value

Point 4. on one of the illustrations above shows the case of functions that bring the value from the elevated level to the regular level.

In FP speak, reducing a list of values into a single value is called fold or reduce. In .NET we have LINQ’s Aggregate. Such function takes an accumulator and a reducer function.

This functionality could also be useful when we want to combine multiple functions into one function. A good example is validation. We could have multiple functions that validate a request, but we’d want to have just one entry point to execute them.

public static Validator<T> CombineValidators(IEnumerable<Validator<T>> validators) =>
  t => validators.Aggreagate(Valid(t), (acc, validator) => acc.Bind(_ => validator(t)));

References

© 2023 Marcin Jahn | Dev Notebook | All Rights Reserved. | Built with Astro.